Generalized linear model

Future Crops Statistical Workshop

Patrick Li

RSFAS, ANU

Content summary

  • Review of linear model
  • Motivation: why beyond linear model?
  • Generalized linear model
  • Example: GTA analysis

Review of linear model

Linear model

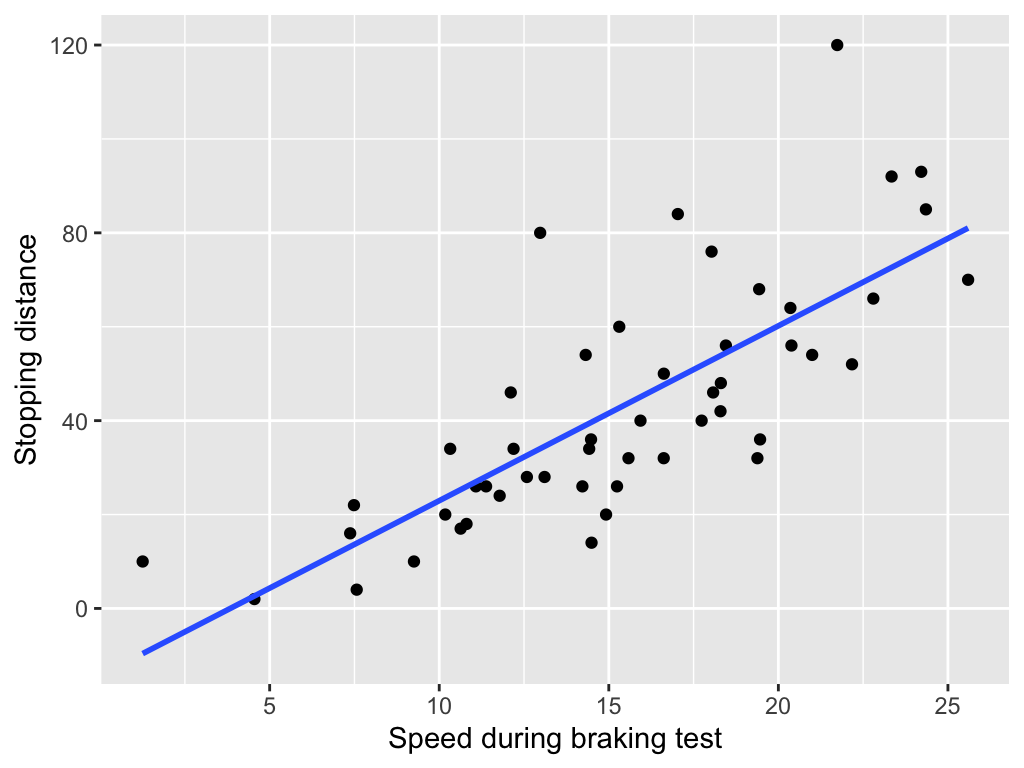
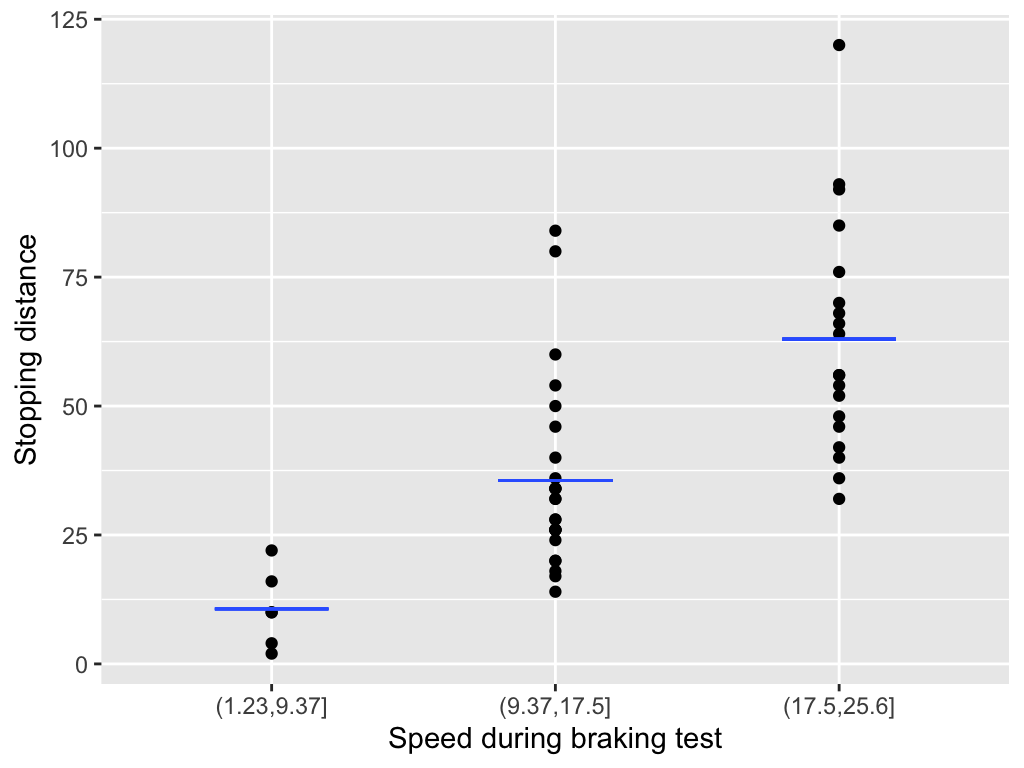
We use linear model (LM) to find the linear relationships between predictor(s) X and a response variable Y.

When the predictor is numerical, the LM fits a straight line through the data that best predicts Y from X.

When the predictor is categorical, the LM estimates the mean of Y for each group or level.

Simple linear model

Mathematically, a simple linear model can be written as

y_i = \beta_0 + \beta_1 x_i + \varepsilon_i, \quad \varepsilon_i \sim N(0, \sigma^2), \quad i = 1, \dots, n,

where \varepsilon_i represents the random error term, the part of y_i that the model cannot explain from x_i.

Maximum likelihood estimation

For a given intercept \hat{\beta}_0 and slope \hat{\beta}_1, the likelihood L(\boldsymbol{\beta}) quantifies how well the observed data fit the model. We can obtain the optimal \hat{\beta}_0 and \hat{\beta}_1 by maximizing L(\boldsymbol{\beta}):

(\hat{\beta}_0, \hat{\beta}_1) = \arg\max_{\beta_0, \beta_1} L(\boldsymbol{\beta}),

which is called maximum likelihood estimation (MLE).

Use the sliders to find the optimal Intercept and Slope!

Why linear models aren’t enough

Just because a cat can fit into a glass doesn’t mean the cat is glass-shaped!

Figure source

We don’t use linear models because they are truly “correct”. In most cases, they’re not.

We use them mainly because of:

  • Convenience
  • Good enough as an approximation
  • Familiarity
  • Computational feasibility
  • … and other practical reasons

Motivation: Why go beyond linear models?

Binary data

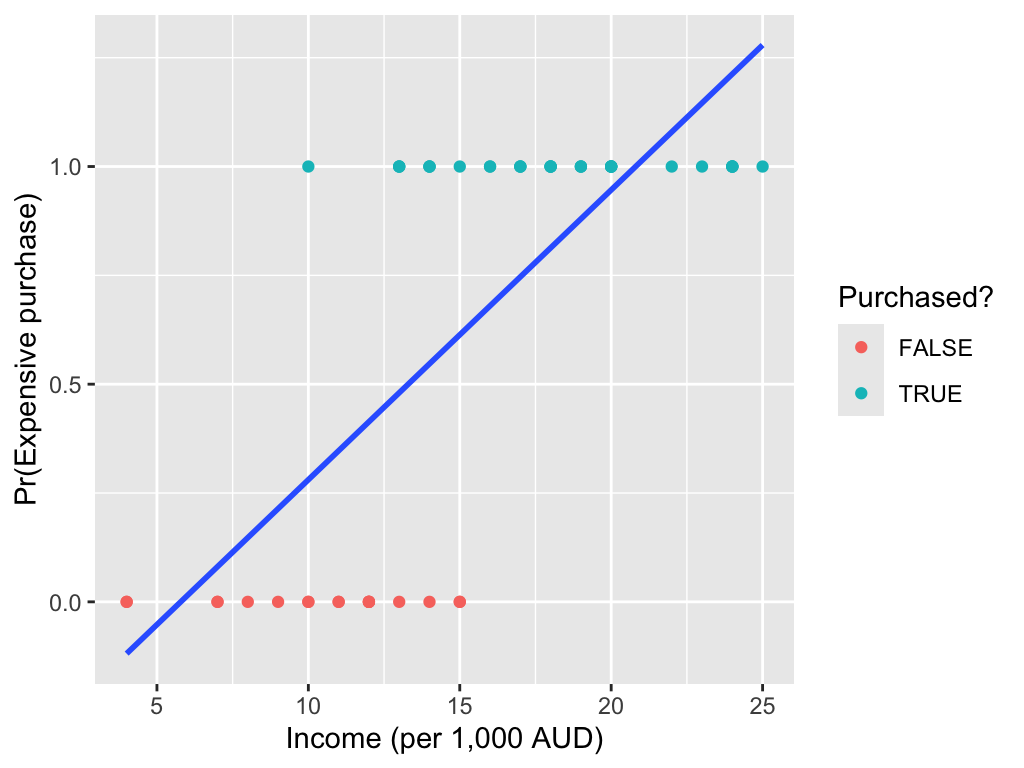
Fitting a linear model is often inappropriate for many types of response variables. For example, with binary data:

Linear models can predict probabilities outside the [0, 1] range.

Count data

With count data:

Linear models don’t work well for low-count data because they can’t capture its skewed shape and may produce negative predicted values.

Generalized linear model

Exponential family

Generalized linear models provide a flexible framework for modeling data whose distribution belongs to the exponential family.

Model components

A generalized linear model (GLM) has three key components:

  • The response Y follows a distribution from the exponential family.
  • A linear predictor, for example, \eta = \beta_0 + \beta_1 X.
  • A link function g\big(E(Y \mid X)\big) = \eta.

Canonical link function

A GLM can use different link functions for the same distribution, but there is always one preferred link that gives particularly nice mathematical properties. This is called the canonical link function.

Common generalized linear models

Distribution Support Typical uses Link name Link function g(\mu)
Normal (-\infty, +\infty) Linear-response data Identity g(\mu) = \mu
Exponential (0, +\infty) Exponential-response data, scale parameters Negative inverse g(\mu) = -\mu^{-1}
Gamma (0, +\infty) Positive continuous outcomes Inverse g(\mu) = \mu^{-1}
Inverse Gaussian (0, +\infty) Skewed positive continuous outcomes Inverse squared g(\mu) = \mu^{-2}
Poisson {0,1,2,\dots} Count of occurrences in fixed time/space Log g(\mu) = \ln(\mu)
Bernoulli {0,1} Outcome of single yes/no occurrence Logit g(\mu) = \ln\frac{\mu}{1-\mu}
Binomial {0,1,\dots,N} Count of “yes” out of N trials Logit g(\mu) = \ln\frac{\mu}{N-\mu}
Categorical [0,K) Outcome of single K-way occurrence Generalized logit g(\mu) = \ln\frac{\mu_1}{1-\mu_1}

Simple poisson regression

A simple Poisson regression can be expressed as

Y_i \sim \text{Poisson}(\lambda_i), \quad \log(\lambda_i) = \beta_0 + \beta_1X_i, \quad i=1,\dots,n.

We then estimate \hat{\beta}_0 and \hat{\beta}_1 by maximizing the likelihood.

Use the sliders to find the optimal \beta_0 and \beta_1!

Deviance

In generalized linear models, the deviance D measures how far our model is from a perfect fit. It is defined as a transformation of the likelihood L:

D = 2\big(\log L(\hat{\theta}_s) - \log L(\hat{\theta})\big),

where L(\hat{\theta}_s) is the likelihood of the saturated model, a model that fits each observation y_i perfectly for i = 1, \dots, n.

Use the sliders to find the optimal \beta_0 and \beta_1!

Deviance test

In a GLM, we can test the null hypothesis H_0: \beta_1 = 0 against the alternative H_1: \beta_1 \neq 0. Under H_0, D_R - D_M \sim \chi^2_1, where D_R is the deviance of the restricted model (excluding \beta_1) and D_M is the deviance of the full model. The degree of freedom of the \chi^2 correspond to the number of parameter restrictions imposed.

To perform the test, we compute the test statistic X^2 = D_R - D_M, and compare it to the critical value of the \chi^2_1 distribution, \chi^2_{1,1-\alpha}.

  • \chi^2_{1,1-0.1} \approx 2.706
  • \chi^2_{1,1-0.05} \approx 3.841
  • \chi^2_{1,1-0.01} \approx 6.635

Simple possion model (deviance test)

Model Description Deviance DOF
\log(\lambda_i) = \beta_0 A constant model where the mean response is the same for all observations. 268.502 199
\log(\lambda_i) = \beta_0 + \beta_1 x_i A model where the log of the mean response is a linear function of the predictor. 248.672 198

Since

D_R - D_M = 268.502 - 248.672 = 19.83 > \chi^2_{1, 0.95},

we reject the null hypothesis H_0: \beta_1 = 0.

Recap of the GTA data

  1. In the GTA analysis, each sample (s), either pure or a fixed admixture, such as GTAMix1 (85% BASS, 15% Maximus CL), is evaluated.

  2. For each sample, multiple devices (d) are tested, and each evaluation produces predictions for one or more varieties (v), for example, (80% BASS, 20% Maximus CL).

  3. Note that for the same evaluations, we sometimes have replicates (r).

  4. These predicted percentages can be converted into predicted counts using the number of seeds actually classified (n_{sdr}) by the device in that evaluation.

Device consistency

We assess the consistency of device predictions by fitting a Poisson model:

n_{svdr} \sim \text{Poisson}(\lambda_{svdr}),\quad\log(\lambda_{svdr}) = \log(n_{sdr}) + \alpha_{vsdr},

where n_{svdr} is the number of predicted seeds of a variety evaluated by a specific device in a given sample and replicate, and n_{sdr} is the total number of seeds classified by that device in the same sample and replicate.

Unrestricted model

Rewriting the model gives:

\begin{align*} \log\big(\lambda_{svdr}\big) - \log(n_{sdr}) &= \alpha_{vsdr},\\ \log\left(\frac{\lambda_{svdr}}{n_{sdr}}\right) &= \alpha_{vsdr}, \end{align*}

which represents the log of the expected percentage of a variety in a sample estimated by the model, for example, 82.2% BASS in GTAMix1.

By including \alpha_{vsdr} in the model, we allow this estimated percentage to vary across variety, sample, device and replicate.

Restricted model

Next, we consider a restricted version of this model

n_{svdr} \sim \text{Poisson}(\lambda_{svdr}),\quad\log(\lambda_{svdr}) = \log(n_{sdr}) + \alpha_{vsr}.

In this version, \alpha is not allowed to vary across devices, effectively imposing constraints on the model parameters. Hence, we refer to it as the restricted model.

Tesing device consistency

Model Description Deviance DOF
\quad\log(\lambda_{svdr}) = \log(n_{sdr}) + \alpha_{vsr} \alpha varies by variety × sample × replicate but not across devices. 70.062 324
\quad\log(\lambda_{svdr}) = \log(n_{sdr}) + \alpha_{vsdr} \alpha varies by variety × sample × device × replicate. 0.000 0

Since

D_R - D_M = 70.062 - 0 = 70.062 > \chi^2_{324, 0.95},

we reject the null hypothesis that device predictions are consistent.

Takeaways

  • Linear models work well for continuous, normally distributed data but can fail with binary or count outcomes.
  • GLMs extend linear models to handle diverse data from the exponential family using link functions.
  • Model evaluation uses deviance to measure fit, with deviance tests comparing nested models.

Thanks! Any questions?

tengmcing

[email protected]

patrickli.org

Slides URL: https://fc-glm.patrickli.org/ | Canberra time